back propagation

神经网络的训练本质上是一个参数的最优化问题，Back propagation(BP)算法在这个过程中起了至关重要的作用。它极大地降低了代价函数对参数的导数计算量。BP如果简单来说的话，其实可以简单：对求导的链式法则的有效利用。然而，体会其中的妙处还得仔细推算一遍。

forward propagation

我们先暂时放下BP，借用Colah君的一个例子，从Forward Propagation开始。假设变量$a,b,c,d,e$有如下的计算关系，我们要计算e对所有其它变量的导数。

$c=a+b$

$d=b+1$

$e=c*d$

下面的计算图表示了上述运过程，每一个节点代表一个变量，节点之间的边代表了变量之间的依赖和影响关系，边上的weight由偏导数定义。

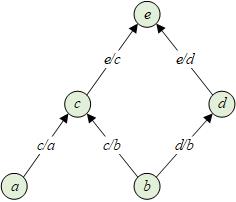
导数可以理解为变量变化$\Delta x$，导致$y$的变化有多大，导数表示了变化速率。这样以来，上图中$\partial e/\partial b$可以通过累加所有从$b$到$e$的path得到，每条path的总weight由各段路径的weights乘积表示。

$\frac{\partial e}{\partial b}=\frac{\partial e}{\partial c}\frac{\partial c}{\partial b}+\frac{\partial e}{\partial d}\frac{\partial d}{\partial b}$

至此，我们的结论是：

任意$y$关于$x$的偏导数，可以通过累加所有$x$影响$y$的路径得到。

这就是forward propagation以及计算图表示清晰地展示给我们的，实际上也是对chain rule的一种直观理解。

back propagation

在forward propagation中，为了计算$e$关于$a,b,c,d$的导数，需要我们分别以$a,b,c,d$为起点，最终走到$e$，计算图中的有些路径被重复走了很多次。避免这个问题的方法是从上往下计算，即从bottom-up模式转换为top-down。这样遍历计算图一次，就可以计算出所有$e$关于$a,b,c,d$的导数。

这种计算方法就是back propagation：仿佛变化量$\Delta$是从被影响变量反向传播到影响他们的变量上。所以，bp本质是一个降低整体求导复杂度的优化算法，之所以谈神经网络必谈bp，是因为nn的参数非常多，如果通过简单的forward方式计算梯度，会导致巨大的计算量。bp因此成为了nn优化的“标配”。