Logistic Regression和分类

Logistic regression（LR）由David Cox在1958年提出，已有近60岁了。它简单、实用，直到今天，仍然是解决分类问题的一个常用方法，在很多领域和系统（如线搜索广告、推荐系统）中都有重要应用。习惯不同，不同文献对它的称呼有所不同：

LR本身是一个二分类模型。对于给定的输入，输出它属于类别正例（positive）还是反例（negative）。
LR的多分类推广称为Multinomial Logistic Regression，支持大于两个类别。LR是Multinomial LR的一个特例。
Multinomial LR使用softmax function后的value来计算代价，又常被称为Softmax Regression。
如果从信息论角度来看Multinomial LR，它又被称为最大熵算法（Max Entropy，ME）。

下文我们将只讨论更为一般的Multinomial LR。同时，为了保持简洁，将统一使用LR来指代Multinomial LR。

LR模型结构

LR对输入样本 $x$ 的分类过程包括三个步骤：

特征化
线性变换
softmax

特征化

特征化（featurization or vectorization）是几乎所有机器学习算法的第一步。它将原始的输入数据（例如图像、文本等）转换成规范统一的数学结构，便于进一步进行计算处理。

特征化依赖提前定义好的各种特征，这些特征直接或者间接地来自对训练数据的观察。以“判断一个自然语言的query是否在询问天气”这个短文本分类问题为例，假设我们的训练预料如下：

beijing weather       positive
what is the weather   positive
beijing time          negative

抽取其中的每个词作为feature，就得到了称为unigram的feature。将他们编号：

0 beijing
1 weather
2 what
3 is
4 the
5 time

现在，对于任意给定的输入query，可以被转换为一个6维的向量，向量的第 $i$ 维为1代表id为 $i$ 的feature被触发，否则为0。

beijing weather     -> [1, 1, 0, 0, 0, 0]
what is the weather -> [0, 1, 1, 1, 1, 0]
beijing time        -> [1, 0, 0, 0, 0, 1]

这样，我们就完成了输入样本的向量化，也就是特征化。该向量在后续的处理流程中完全代表了输入样本。

特征的抽取对包括LR在内的所有机器学习算法都至关重要，特征的质量决定了算法的表现。在上面的例子中，我们只使用了unigram作为feature，它无法表征词的顺序和先后位置信息，通常还需要bigram（连续两个词），trigram（连续三个词）甚至更高阶的上下文。除此之外，还有很多可以想象的feature，例如：

有没有词出现在一个预先搜集的地名列表中
句子的长度信息

特征的提取是一个开放的问题，依赖经验和实验尝试。总的来说，提供的不相关特征越多，越能区分不同的类别，就越可能得到较好的分类效果。

线性变换

得到样本的向量表示 $x$ 之后，LR对其进行线性变换：

$z=wx+b$

其中的变量均为矩阵或向量，记x的维度（也就是特征个数）Dim(x)=m，分类的类别数为n，则各变量的维度如下：

w : n*m
b : n*1
z : n*1

$z$ 的每一维代表一个类别的得分，得分最高的类别就是分类结果。

softmax

softmax函数 $y=\text{softmax}(z)$ 将任意实数表示的向量 $z$ 变换为向量 $y$ 。 $y$ 的每一维都是一个介于(0,1)之间的实数，且所有维度上的值和为1。因此，可以将 $y_i$ 理解为 $x$ 属于类别 $i$ 的概率 $P(y=i|x)$ 。

softmax变换是一个单调变换，并不会改变 $z$ 在不同维度上取值的相对大小，因此对判别 $x$ 所属的类别没有意义。变换的目的在于下文要提到的训练过程。

训练

以上LR模型中包含着很多未知的参数，包括线性变换的矩阵 $w$ 和bias向量 $b$ 。对于给定的训练样例，得出最优的参数取值的过程称为模型训练。

训练的过程分为两步：

设计代价函数。
最优化参数求解。

代价函数

代价函数是模型输出结果和真实标注结果之间误差的度量。LR使用cross entropy作为代价函数。对于给定的n组训练样例 $((x^{(0)},y^{(0)}),...,(x^{(n-1)},y^{(n-1)}))$ ，代价函数

$C=\sum_{i}D(y{'}^{(i)},y^{(i)})=-\sum_{i}\sum_{j}y_j^{(i)}\cdot\log y_j{'}^{(i)}$

其中 $y'$ 为模型输出， $y$ 为真实标注。

相比cross entropy，均方误差其实是一个更加直观的代价函数。但是由于softmax函数的性质，会使得参数 $w$ 和 $b$ 的更新缓慢。而cross entropy没有这个问题，作为代价函数更为常用。

为了防止过度拟合训练数据，代价函数通常还会加上一项正则项（regularization），通常为 $|w|$ 或 $||w||^2$ ，分别称为l1、l2 norm/penatly/regularization。最终的代价函数如下， $\alpha$ 控制了regularization项在代价中的权重。

$\text{L2: } C=-\sum_{i}\sum_{j}y_j^{(i)}\log y_j{'}^{(i)}+\frac{1}{2}\alpha||w||^2$

$\text{L1: } C=-\sum_{i}\sum_{j}y_j^{(i)}\log y_j{'}^{(i)}+\alpha|w|$

最优化参数

Batch Gradient Descent

对于已知的固定训练数据，代价函数C是关于 $w$ 和 $b$ 的函数，而且是一个凸函数，即存在全局最优解。求解这个最优解的一个最常用迭代算法称为梯度下降（Batch Gradient Descent）。

Choose an initial vector of parameters w and learning rate \eta.
Repeat until an approximate minimum is obtained:
    Randomly shuffle examples in the training set.
    do:
        w := w - \eta \nabla C(w,b).
        b := b - \eta \nabla C(w,b).

Stochastic Gradient descent

Gradient descent的复杂度相当高。 $w$ 和 $b$ 的每一次更新，都必须遍历所有的training data。一个更加常用的训练算法是统计梯度下降（Stochastic gradient descent,SGD）。相比Batch Gradient Descent要全部遍历一遍训练数据才能更新一次参数，SGD则每见到一个训练数据之就更新一次参数。

采用SGD时，代价函数不再是对所有training samples的加和，而是只计算当前样例：

$C=-\sum_{j}y_j^{(i)}\log y_j{'}^{(i)}+\frac{1}{2}\alpha||w||^2$

Choose an initial vector of parameters w and learning rate \eta.
Repeat until an approximate minimum is obtained:
    Randomly shuffle examples in the training set.
    For \! i=1, 2, ..., n, do:
        w := w - \eta \nabla C(w,b).
        b := b - \eta \nabla C(w,b).

SGD由于自身的特点和优势，是目前广泛使用的参数优化方法：

更加快速。每遍历一个训练样例就更新参数是一个极端的例子，通常可以每遍历m个训练样例更新一次参数，一定程度上减少单个样例带来的偏差。这个m通常称为mini-batch。
行之有效。它通常可以逼近最优解。简单来讲，当训练数据量足够多时，单个训练样例带来的偏差最终会被整体数据的分布趋势所纠正和覆盖。
易于并行化。例如将数据分割为n份，n个线程各取一份数据并行运行SGD，再将各自训练出的参数进行average。或者各个线程以异步方式更新一组共享于parameter server的参数，google的word2vec就采用了这种方式。

其它优化算法

mini-batch SGD尽管很常用，但是也存在很多问题。例如，如果我们仔细考虑SGD的梯度下降过程：

$\theta=\theta - \eta \nabla C(\theta)$

会发现我们是用参数减去参数的梯度，二者的单位其实都不同。SGD实际利用的仅仅是极值相对于当前值的方位信息，这一方位由梯度的方向指出，在求解过程中有可能出现在极值附近来回震荡的情况。

类似的细节问题还有很多，针对这些问题，有很多其它的改进或优化方法，例如：

Momentum
Nesterov accelerated gradient
Adagrad
Adadelta
RMSprop
Adam

包括SGD在内的这些最优化方法不仅可以用于训练本节提到的LR，SVM等存在全局最优点的问题，也同时广泛应用在神经网络等多极值问题中。

概率解释

到这里，LR的所有重要细节都已经展现在我们面前了。最后要问的问题是，为什么LR是行之有效的分类方法呢？LR有其数学解释。从概率论角度，一个直接、合理地代价函数应该定义为：建模分类正确的概率。假设训练数据 $(x^{(0)},y^{(0)}),...,(x^{(n-1)},y^{(n-1)})$ 服从独立同分布（identical independent distribution,i.i.d.），则分类正确的概率为：

$p(y^{(0)},...,y^{(n-1)}|x^{(0)},...,x^{(n-1)};w,b)=\prod\limits_{i} p(y^{(i)}|x^{(i)};w,b)$

这个概率被称为后验概率，它是关于参数 $w$ 和 $b$ 的函数，统计学上称为似然函数（likelihood）。对它取对数值，将乘法转换为加法，就得到对数似然函数（log likelihood）：

$L(w,b)=\log p(y^{(0)},...,y^{(n-1)}|x^{(0)},...,x^{(n-1)};w,b)=\sum\limits_{i}\log p(y^{(i)}=k^{(i)}|x^{(i)};w,b)$

可以看出，LR的cross entropy代价函数实际上就是该对数似然函数 $L(w,b)$ 。训练样例真实标注 $y$ 是一个只有在真实类别k对应的维度上为1，其它维度全0的向量。这样以来，cross entropy其实就是 $y'$ 在维度k上的取值 $y_k'$ 的log值。因此，最大化cross entropy，就是在最大化对数似然函数，也即最大化后验概率。像LR这种直接建模后验概率 $p(y^{(i)}|x^{(i)})$ ，而不是样本联合分布 $p(x^{(i)},y^{(i)})$ 的模型，通常被归为判别式模型（discriminative model）。

LR vs SVM

在分类方面，另一个被认为是效果最好的分类算法是SVM，它无论在理论上还是在工程实现上都堪称完美。SVM的代价函数定义如下:

$\max \frac{1}{||w||}, s.t., y^{(i)}(w^Tx^{(i)}+b)\ge1,i=0,...,n-1$

这一代价函数也是一个有全局最优解的凸函数，优化这个带有约束条件的复杂代价函数的过程，可以通俗的解释为：找到两个平行的超平面a和b，使得正例和反例分别全部处于a和b的一侧，且a和b的距离最大。此时，a和b的正中间1/2处的超平面就是最优的 $w$ 和 $b$ 定义的平面

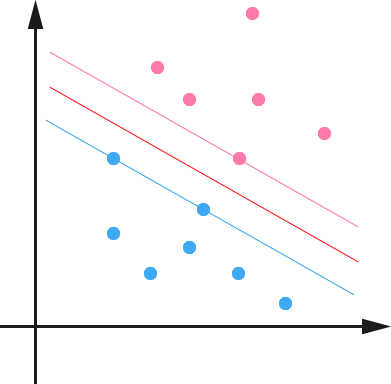
实际中，严格可分（称为hard-margin）的情况通常不太常见，我们需要能够容忍一定量的噪声样例。考虑到这一点，我们引入hingle函数，它对于分类正确的样例值为0，对于错分的样例有一定的惩罚（称为soft-margin）。最终，SVM的代价函数可以等价变化为如下形式，并且摆脱了约束条件。

$\text{SVM: }\min\limits_w\frac{1}{2}\alpha w^Tw+\sum\limits_i\max(0,1-y^{(i)}(w^Tx^{(i)}+b)),y \in \{+1,-1\}$

此时，我们的第一个发现是，SGD等优化方法同样可以用来训练SVM，尽管SVM漂亮的理论使得它有其它漂亮实用的训练方法coordinate descent。

第二点，我们对比LR的代价函数：

$\text{LR: } \min\limits_w\frac{1}{2}\alpha w^Tw+\sum\limits_{i}\log(1+e^{-y^{(i)}(w^Tx^{(i)}+b)}),y \in \{+1,-1\}$

可以看出，二者的差别其实就是 $\log(1+e^{-x})$ 和 $\max(0,1-x)$ 的差别。实际上，二者的差距并不算很大，所以可以预期LR和SVM在线性分类上效果是可比的。

线性可分性

到这里，我们一直讨论的是线性分类方法。这些方法能够奏效的前提是问题本身线性可分。那如何知晓一个问题是不是线性可分问题呢？一个可以用来度量的依据是特征维度和样本个数的关系。

我们把特征想象成空间坐标系，样本则是坐标系中的点。首先考虑一个简化的问题：二分类，两个特征维度。在不共线的情况下，这个二维坐标系中的任意三个样本点，无论标注如何，一定是线性可分的，到了四个点就有可能不可分了，我们称这个数字为最大可分样本数。二维特征空间的最大可分点数为3，推而广之，n维特征空间的最大可分点数至少是大于n的。

对于一些特征非常丰富的问题，例如自然语言分类，有效样本增加一个带来的特征增加通常大于1，可以预期，特征数通常大于样本数，因此属于线性可分问题。这一判定的意义在于给我们可以使用简单、快速的线性分类方法来解决问题提供了一定的可行性支撑。

Logistic Regression和分类